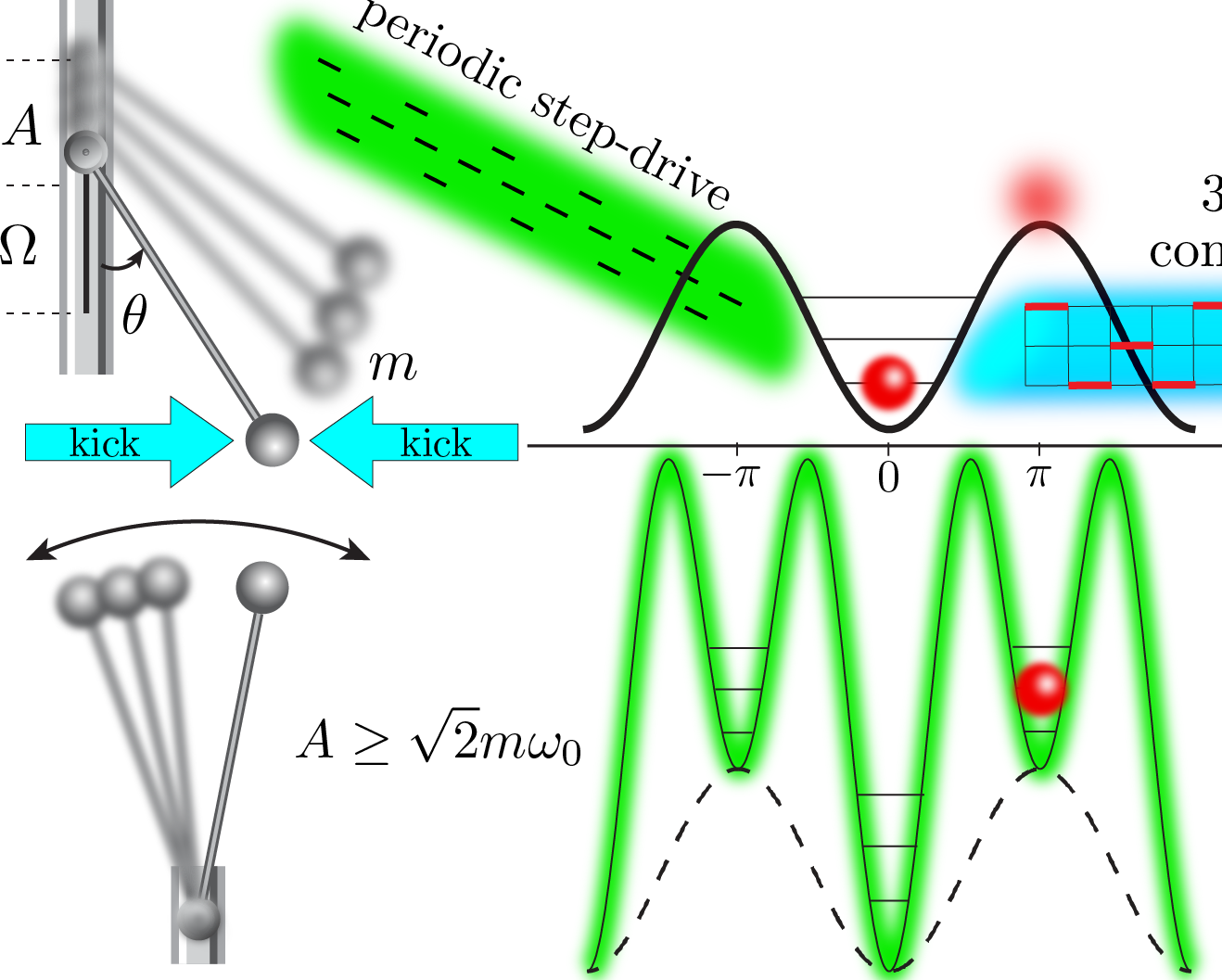
A physical way to characterize the complexity of preparing quantum states is the quantum speed limit – the minimal time required to prepare a target state with unit fidelity. We formulated a Conjecture according to which, for any protocol within the space of available controls, the time-integrated energy fluctuations are bounded from below by the adiabatic geodesic length between the initial and final states.

Our results imply that the adiabatic limit, in which the conjectured bound is tight, puts a fundamental constraint on the minimal duration of any unit-fidelity protocol, even those which excite the system far away from equilibrium at intermediate times. Check out this paper for a more detailed and complete discussion [1].

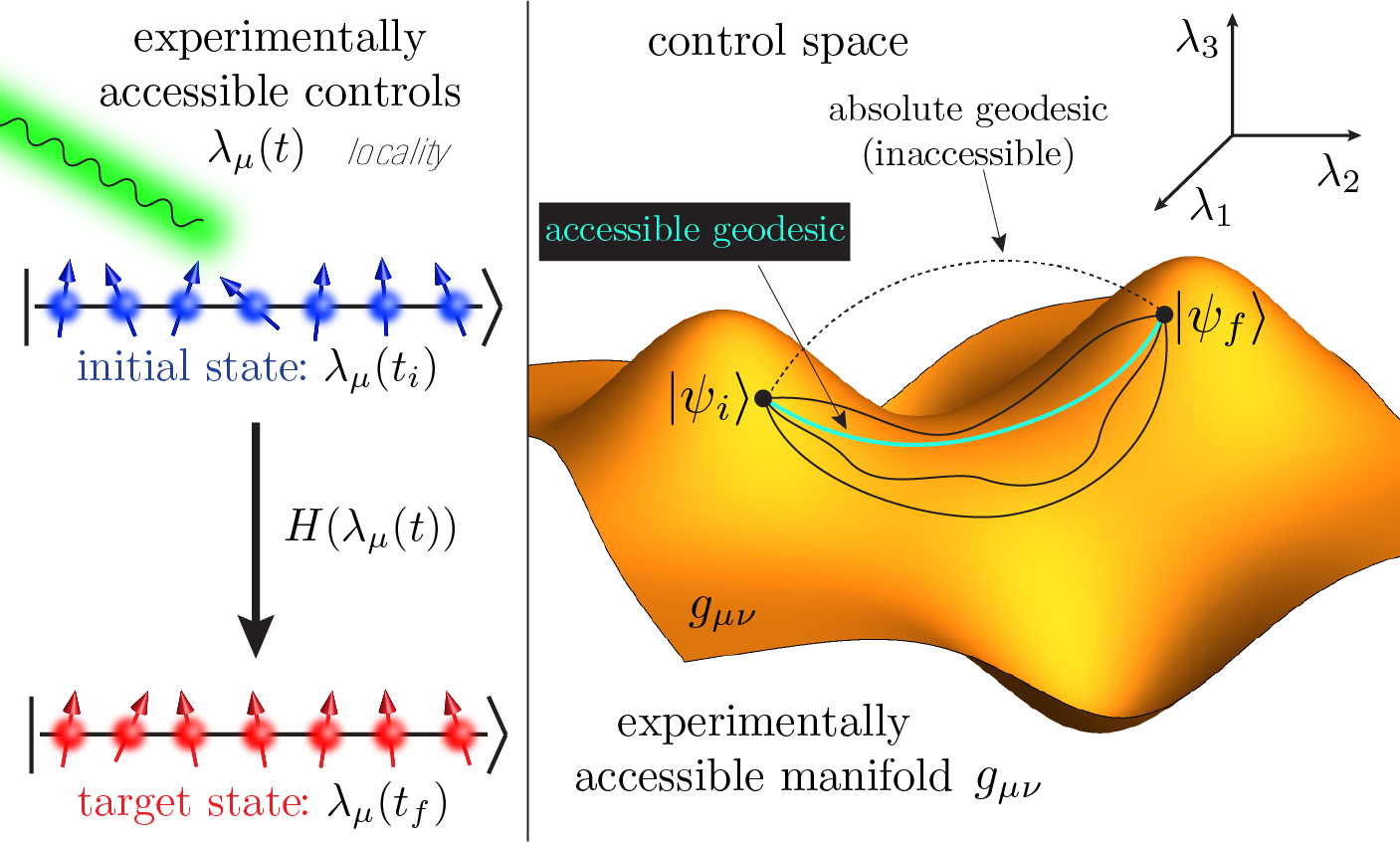
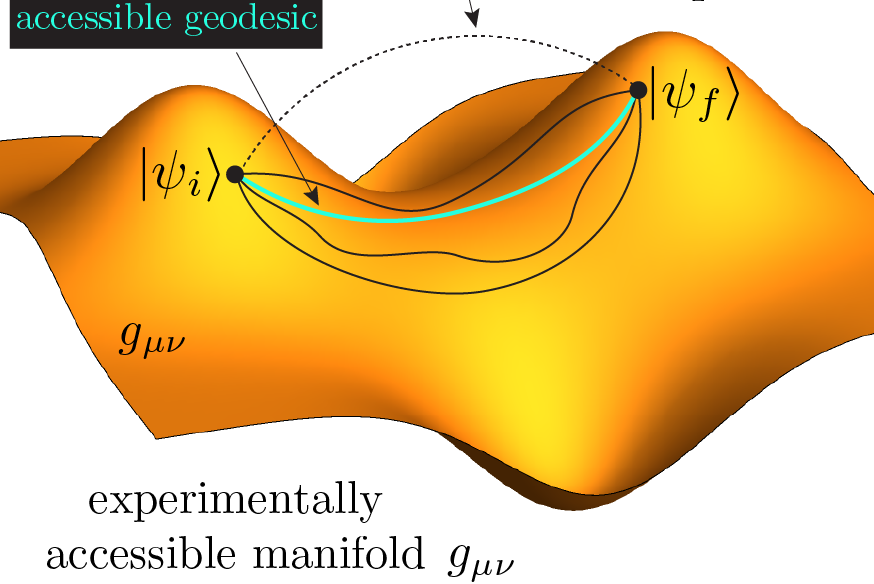
Advances in quantum computing depend on the ability to reliably manipulate quantum states. One way to characterize the complexity of this ability is the “quantum speed limit,” the minimal time required to generate a quantum state from some initial condition (see Fig, left panel). This time is limited by the energy fluctuations created in the system: the larger the energy fluctuations, the shorter the quantum speed limit, and the faster a state can be prepared. Since energy variance increases as more particles are added to the system, this deceptively suggests that the quantum speed limit goes down as the system size increases. Here, we resolve this conundrum by considering additional constraints that are present in experimentally realizable systems.

We present numerical and analytical evidence of a new lower bound on the energy fluctuations—and hence the quantum speed limit—that is controlled by the geodesic distance, a parameter that describes how “far apart” two quantum states are in the control space (see Fig, right panel). Since energy variance is an extensive quantity, this may deceptively suggest that in many-body systems the quantum speed limit goes down with increasing system size. We resolve this issue by taking into account constraints imposed by the locality of experimentally realizable control Hamiltonians.

We also investigate and analyze the effects of such constraints on the quantum speed limit. According to our conjecture, for any protocol confined to the space of available controls, the time-integrated energy fluctuations are bounded from below by the adiabatic geodesic length between the initial and the final state. This length is much larger than the absolute distance between these states [2]. In particular, in extensive systems with local interactions the adiabatic geodesic length typically scales as a square root of the system size if we target gapped ground states. However, the adiabatic geodesic length can increase much faster (e.g. exponentially) with system size for many-body excited states. We prove our conjecture close to the adiabatic limit, and provide ample analytic and numerical evidence for its validity in multiple systems of various complexity. Practically, the conjecture enables us to provide a much tighter bound to the quantum speed limit than was previously known, relating it to the geodesic length in the accessible control space.

You can find all details in our paper.

References:
[1] M.B., D. Sels, and A. Polkovnikov, Phys. Rev. X 9 011034 (2019).
[2] D. P. Pires, M. Cianciaruso, L. C. Céleri, G. Adesso, and D. O. Soares-Pinto, Phys. Rev. X 6 021031 (2016).
[3] S. Deffner, C. Jarzynski, and A. del Campo, Phys. Rev. X 4 021013 (2014).
[4] K. Funo, J.-N. Zhang, C. Chatou, K. Kim, M. Ueda, and A. del Campo, Phys. Rev. Lett. 118 100602 (2017).
[5] D. Sels and A. Polkovnikov, PNAS 114 3909 (2017).

Copyright © 2019 Marin Bukov