Floquet engineering is an established technique from the quantum simulation toolbox, with the present bottleneck set by unwanted heating. We study the occurrence of Parametric Instabilities in Weakly-Interacting Bosonic Optical Lattices, and showcase the detrimental effects caused by transverse degrees of freedom and weak harmonic traps.

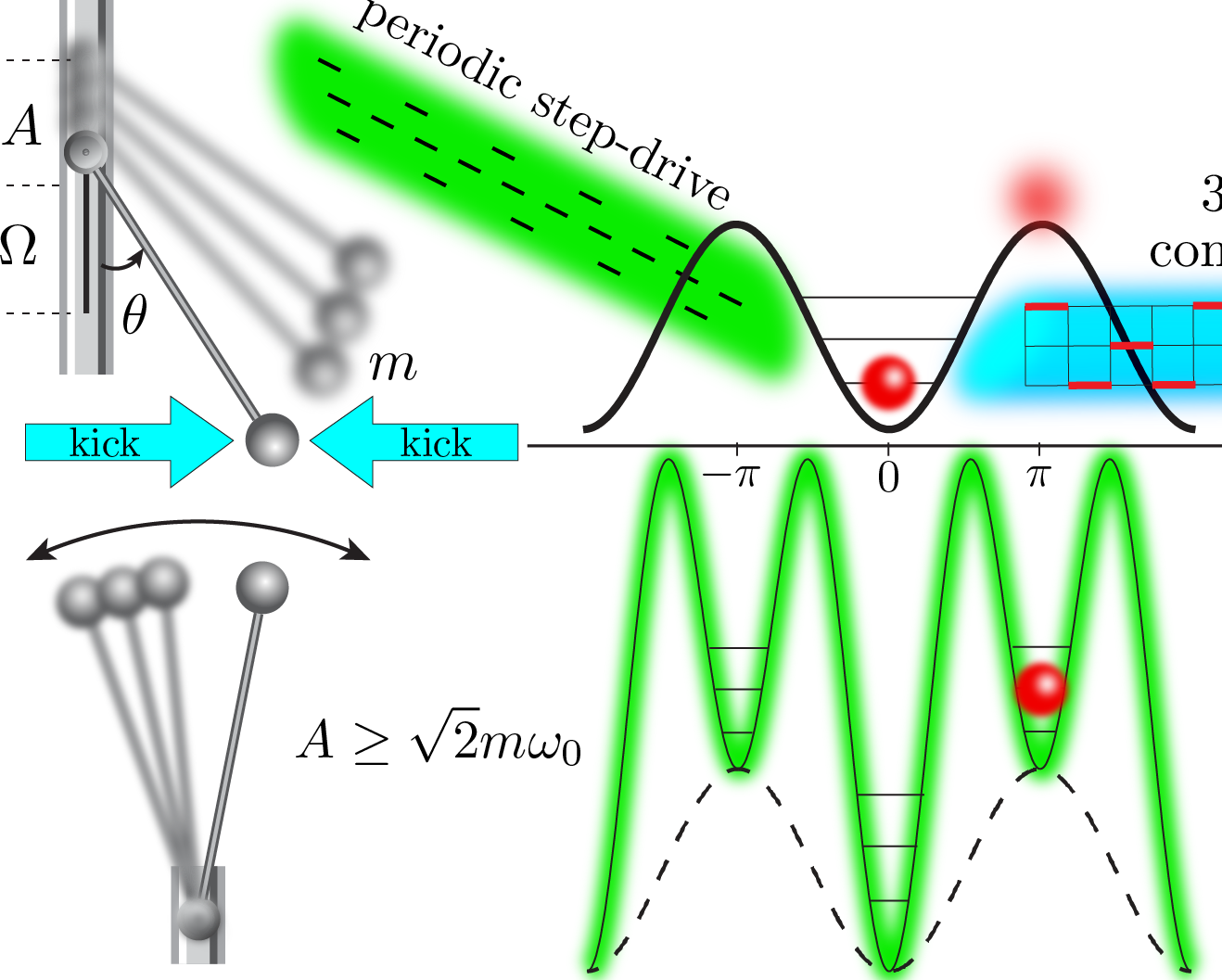
We consider a system of ultracold weakly-interacting bosons in an optical lattice [grey “egg carton”-like structure in Fig above]. The bosons can “hop” between neighboring lattice sites (this phenomenon is caused by quantum mechanical tunneling, but you can think of it as hopping). For every two bosons occupying the same lattice site, there is an additional interaction energy cost. If the (density-renormalized) interaction \(g\) is strong compared to the hopping \(J\), and the number of bosons is commensurate with the number of lattice sites, the bosons are localized in the lattice sites and remain frozen (cannot hop) - this is known as a Mott insulator state. Conversely, whenever the “hopping rate” \(J\) is much larger than the interaction \(g\), kinetic energy dominates and the individual bosons lose their identity: they behave as a macroscopic quantum fluid, known as a superfluid [red blob in the Fig above].
Whenever superfluid systems in experiments are subject to periodic shaking through the underlying optical lattice, they start heating up. Heating is detrimental to cold atom experiments and represents a major challenge to overcome in the quest for quantum simulation, e.g. Floquet engineering [1-3]. Although the relevant scattering processes leading to heating obey the Floquet Fermi Golden Rule [4,5], our knowledge of the heating rates remains incomplete. In a collaboration with the Harvard and Brussels groups, we showed that the short-time behavior of strongly-driven weakly-interacting ultracold bosonic systems is dominated by parametric instabilities of collective excitations in the Floquet-engineered model [6-8]. The theory we proposed was verified in experimental collaborations with groups at the LMU/MPQ [10] and JQI [11].
|
Parametric resonance: a child on a swing uses periodic thrusts to increase the amplitude of oscillation (inset). The same phenomenon is observed in periodically-modulated bosonic optical lattices and leads to unwanted heating at short times. |
Theoretical Predictions: Starting from a superfluid initial state, the short-time dynamics of the periodically-driven system exhibits parametric resonances – a phenomenon familiar from the dynamics of a child on a swing [see video above]. In the same way kids speed up the swing by regular periodic thrusts which rapidly increase the amplitude of oscillations, periodic driving excites bosonic superfluids in optical lattices.
As we live in a three-dimensional space, experiments with low-dimensional optical lattices often possess transverse degrees of freedom (tubes, pancakes). The latter can facilitate heating by supporting states which can be brought on resonance with the external periodic drive. Let us denote the drive amplitude by \(K\), and the driving frequency – by \(\omega\), with the dimensionless ratio \(\alpha=K/\omega\). Using time-dependent Boboliubov de Gennes (BdG) theory, we showed the existence of a qualitative change in the heating rates \(\Gamma\) at a critical drive drequency \(\omega_c\), set by the details of the drive and the dispersion relation of the system.
- for \(\\omega\\leq\\omega_c\), the maximally-instable mode \(q^x_\\mathrm{mum}\) [in units of the lattice constant] and the associated instability rate \(\Gamma\) are given by [\(\\hbar=1\)]:
- for \(\\omega\\geq\\omega_c\), the maximally unstable mode appeats at the edge of the Brillouine zone:
\(\) q^x_{\text{mum}}=\pi \(\)
| \(\) \Gamma= 4J\left | \mathcal{J}_{2}(K/\omega)\right | \dfrac{g}{\omega}_{} \(\) |
For more theory details, check out this paper and this paper.
Experimental Observations:
The Munich experiment [10] was able to observe directly the appearance of the maximally unstable mode by performing a time-of-flight imaging of the superfluid momentum distribution function. This experiment considered a one-dimensional lattice, linearly shaken along the lattice (\(x\)-) direction, in the presence of pancake-like transverse degrees of freedom. The Figure below shows the theoretical perdiction (a) and the experimental measurement (b).
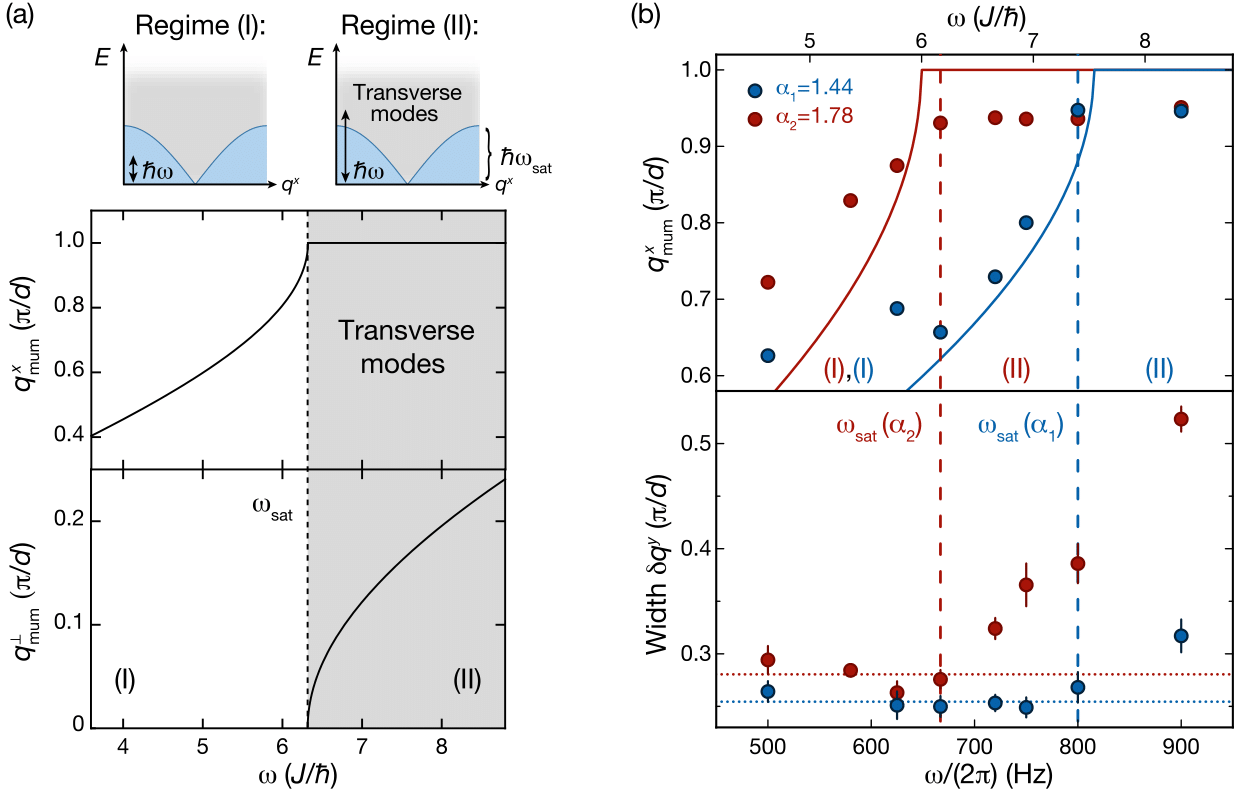
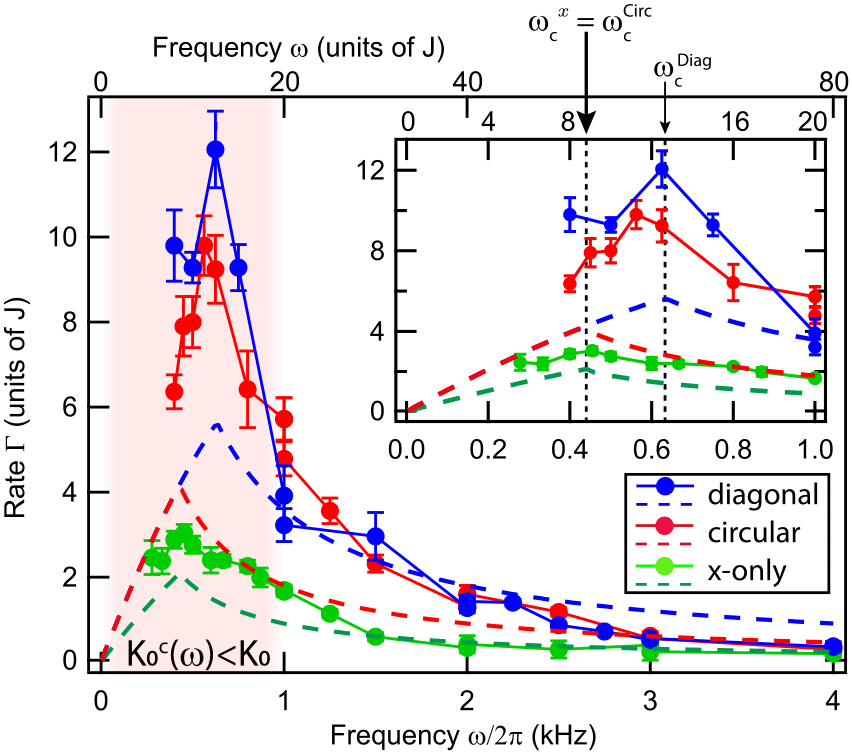
The JQI experiment [11], on the other hand, observed the critical saturation frequency \(\omega_c\) in the behavior of the instability rate \(\Gamma\). This experiment considered one- and two-dimensional lattices in the presence of a tube-like transverse degree of freedom. The optical lattices are modulated using one- and two-dimensional linear (along the \(x\)-direction and the lattice diagonal) and circularly polarized periodic drives. The Figure below shows the theoretical prediction (dashed lines) and the experimental measurement, displaying a clear kink at the critical saturation frequency.
References:
[1] M.B., L. D’Alessio and A. Polkovnikov, Advances in Physics, Vol. 64, No. 2, 139-226 (2015).
[2] N. Goldman and J. Dalibard, Phys. Rev. X, 4, 031027 (2014).
[3] A. Eckardt, Rev. Mod. Phys., 89, 011004 (2017).
[4] T. Bilitewski, N. R. Cooper, Phys. Rev. A 91, 033601 (2015).
[5] M. Reitter, J. Näger, K. Wintersperger, C. Sträter,
I. Bloch, A. Eckardt, and U. Schneider, Phys. Rev. Lett. 119, 200402 (2017).
[6] C. E. Creffield, Phys. Rev. A 79, 063612 (2009).
[7] M.B., S. Gopalakrishnan, M. Knap, and E. Demler, Phys. Rev. Lett., 115, 205301 (2015).
[8] S. Lellouch, M.B., E. Demler, and N. Goldman, Phys. Rev. X, 7, 021015 (2017).
[9] S. Lellouch and N. Goldman, Quantum Science and Technology, 3, 024011 (2018).
[10] J. Näger, K. Wintersperger, M.B., S. Lellouch, E. Demler, U. Schneider, I. Bloch, N. Goldman, and M. Aidelsburger, arXiv:1808.07462 (2018).
[11] T. Boulier, J. Maslek, M.B., C. Bracamontes, E. Magnan, S. Lellouch, E. Demler, N. Goldman, J. V. Porto, Phys. Rev. X, 9, 011047 (2019).
Copyright © 2018 Marin Bukov