Recent surge of activity in Periodically Driven many-body Systems has spawned a new branch of quantum physics, known as Floquet engineering: the synthetic generation of novel Hamiltonians, otherwise inaccessible in static condensed matter systems.
One of the main reasons periodically-driven (Floquet) quantum systems have attracted a lot of attention is that their dynamics can be efficiently described by a time-independent Floquet Hamiltonian $H_F$. Positioned at the border between equilibrium and nonequilibrium, closed Floquet systems represent a natural playground for developing pioneering theories for the phenomena underlying the physics away from equilibrium.
I have been actively studying three main aspects of this ubiquitous field of physics (check out my PhD dissertation):
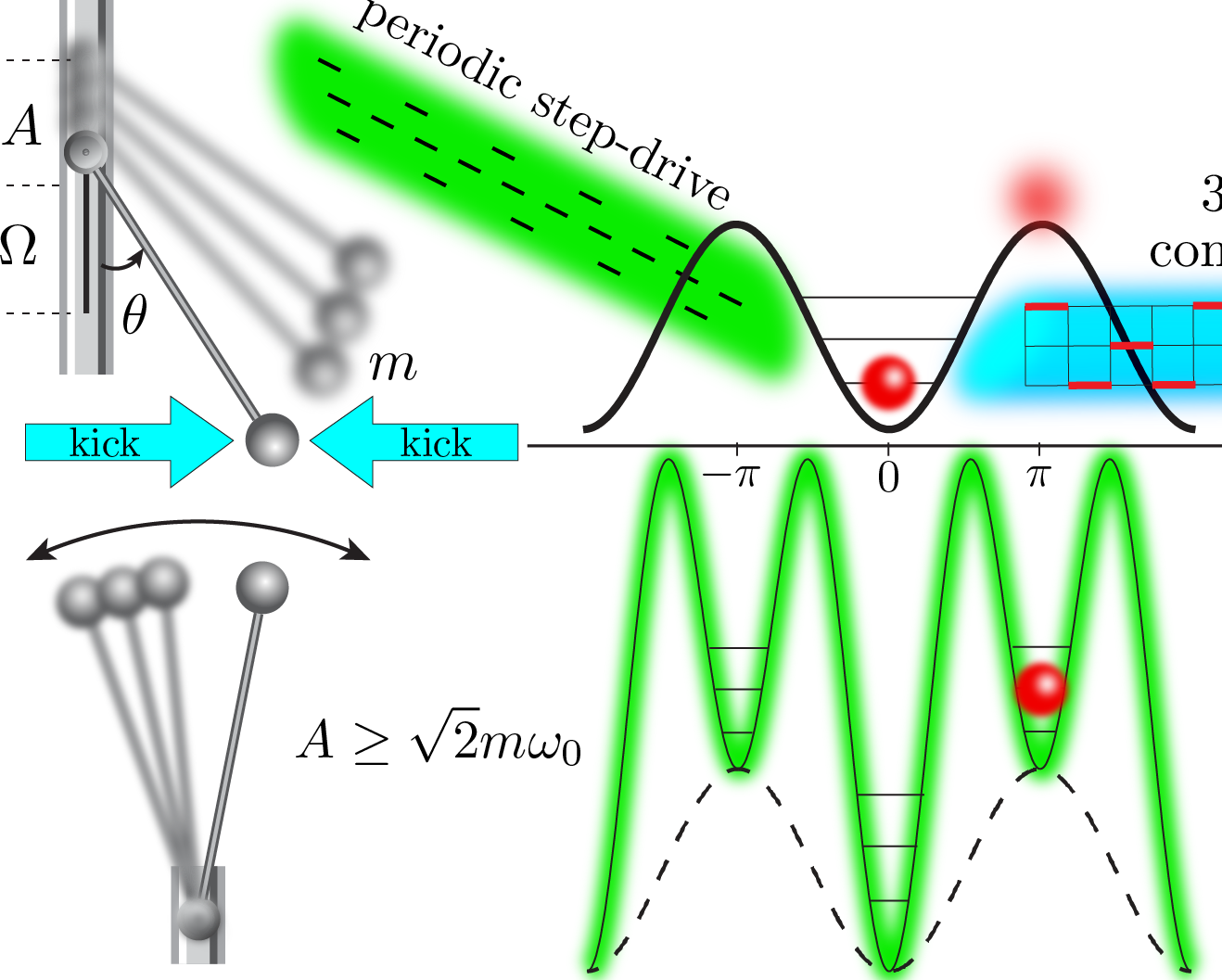
![<i>Floquet realization of the Harper-Hofstadter model [4-6].</i>](/media/posts/floquet.jpg) Floquet Engineering [1-3] encompasses the study how to ascribe novel properties to the effective Floquet Hamiltonian $H_F$ at high drive frequencies (compared to all other energy scales of the problem). One paradigmatic example is the Kapitza pendulum.
Floquet Engineering [1-3] encompasses the study how to ascribe novel properties to the effective Floquet Hamiltonian $H_F$ at high drive frequencies (compared to all other energy scales of the problem). One paradigmatic example is the Kapitza pendulum.
Mastering Floquet Engineering is a difficult problem, since most approaches are typically limited to perturbative and asymptotic expansions of $H_F$. Moreover, it requires the understanding of a fine interplay between virtual (off-shell) and real (on-shell) photon absorption processes, induced by the periodic modulation.
I contributed to this field by writing a review on the topic, systematizing different techniques of Floquet Engineering [1]. I also worked on extending these ideas to strongly-interacting, strongly-driven and resonantly-driven systems [7], which are notoriously harder to study as they do not admit exact closed-form analytica solutions. A major part of my research is focussed on bringing out the nonequilibrium aspect of these systems, and contrasting it to their deceptive equilibrium-like properties.
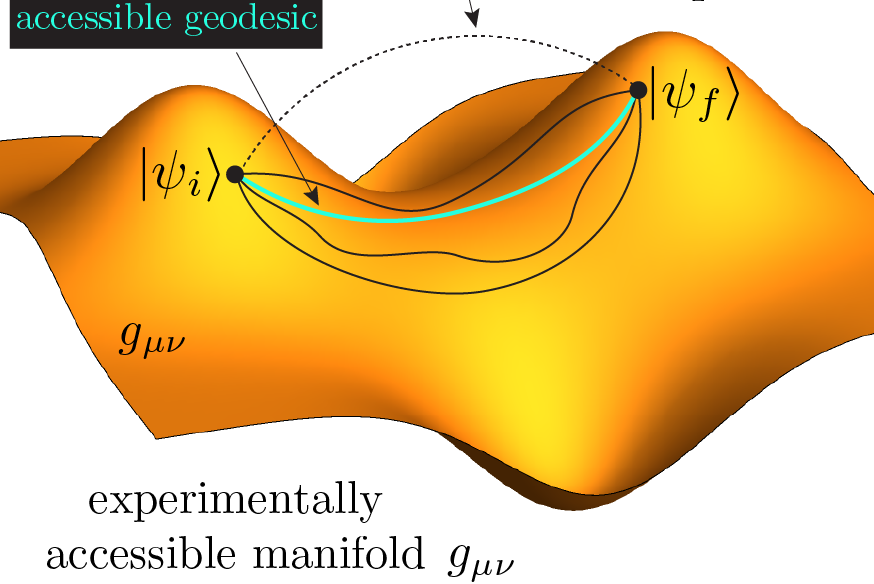
![<i>Adiabatic passage through a photon absorption avoided crossing in the quasienergy spectrum of the Kapitza pendulum. The ground state (red) is hybridized with a higher-energy state (blue) close to the crossing [8].</i>](/media/posts/FAPT.png) Floquet State Preparation. Knowing how to engineer a desired Floquet Hamiltonian appears insufficient in many
experimental situations, since the interesting uderlying physics is not accessible in all of its eigenstates. Therefore, developing a theory for efficiently preparing Floquet states under the presence of periodic modulation can provide a bridge between many theoretical studies and their experimental ralisation.
Floquet State Preparation. Knowing how to engineer a desired Floquet Hamiltonian appears insufficient in many
experimental situations, since the interesting uderlying physics is not accessible in all of its eigenstates. Therefore, developing a theory for efficiently preparing Floquet states under the presence of periodic modulation can provide a bridge between many theoretical studies and their experimental ralisation.
However, Floquet state preparation is a hard, since closed Floquet systems are not coupled to thermal reservoirs, which could provide a bath to dissipate the energy pumped in by the periodic drive during the loading process. Moreover, the adibatic limit is not well-defined either.
I worked on deriving Floquet Adiabatic Perturbation Theory (FAPT) [8] from first principles, extending Linear Response theory and Quantum Geometry to strong periodic drives. We showed that, even though the adiabatic limit may not be well defined, there exist parametrically large regimes where the predictions of FAPT remain valid, even for nonintegrable many-body systems. We analysed the crucial role of resonances for understanding the breakdown of FAPT.
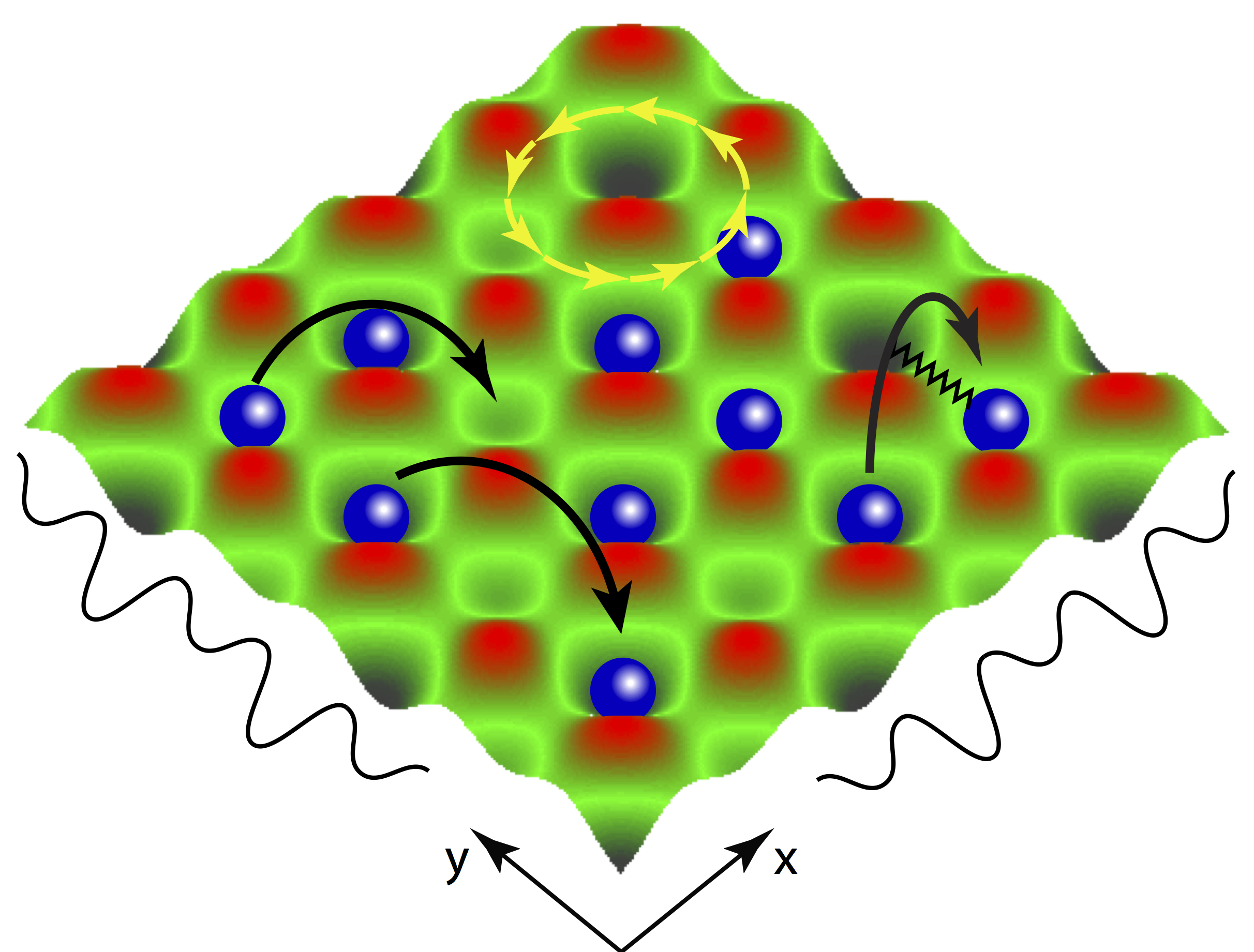
Floquet (Pre-)Thermalization. Assuming we have resolved the issues related to preparing a particular desired Floquet state, the interesting physics it hides can still easily remain elusive if the system absorbs a lot of energy from the perioic drive. Intuitively, one may expect that the periodic modulation pumps energy into the system, and ultimately heats it up to a featureless state. Perhaps surprisingly, at large drive frequencies, energy absorption has been found to be at least exponentially suppressed with the drive frequency [9-10]. This opens up a large window where the system enters a pre-thermal Floquet steady state, captured by the physics of the effective Hamiltonian.
![<i>A pair of many-body Floquet resonances resolved with the infinite-frequency Hamiltonian [13].</i>](/media/posts/floquet_res.png) The study of (pre-)thermal states emerging due to periodic modulation attempts at finding answers to the questions how and under what conditions Floquet systems heat up. This problem is particularly complicated even in equilibrium, since it generically appears for nonintegrable models where analytical control is scarce. Adding to the complexity, the only fully reliable numerical tool to study thermalisation problems is still Exact Diagonalisation.
The study of (pre-)thermal states emerging due to periodic modulation attempts at finding answers to the questions how and under what conditions Floquet systems heat up. This problem is particularly complicated even in equilibrium, since it generically appears for nonintegrable models where analytical control is scarce. Adding to the complexity, the only fully reliable numerical tool to study thermalisation problems is still Exact Diagonalisation.
I studied extensively pre-thermalisation and stability of strongly-driven weakly-interacting bosonic systems, and developed a conserving approximation for weak interactions, mapping out the parametric stability diagram for the periodically-driven Bose-Hubbard model [11-12]. I also made contributions to understanding the microscopic mechanisms behind energy absorption in strongly-interacting many-body quantum systems [13]: at high driving frequencies energy absorption is inhibited by the locality of the Floquet Hamiltonian, and thermalisation is contrained by emergent effective local (quasi-)conserved quantities out to very long times. At low frequencies, on the other hand, a proliferation of many-body resonances, which are non-perturbative in te inverse driving frequency, leads to unconstrained thermalisation, and the system quickly heats up. These two regimes are separated by extremely slow, non-thermalising dynamics.
References:
[1] M.B., L. D’Alessio and A. Polkovnikov, Advances in Physics, Vol. 64, No. 2, 139-226 (2015).
[2] N. Goldman and J. Dalibard, Phys. Rev. X, 4, 031027 (2014).
[3] A. Eckardt, Rev. Mod. Phys., 89, 011004 (2017).
[4] M. Aidelsburger, M. Atala, M. Lohse, J. T. Barreiro, B. Paredes, and I. Bloch, Phys. Rev. Lett., 111, 185301 (2013).
[5] H. Miyake, G. A. Siviloglou, C. J. Kennedy, W. C. Burton, and W. Ketterle, Phys. Rev. Lett., 111, 185302 (2013).
[6] M.B. and A. Polkovnikov, Phys. Rev. A, 90, 043613 (2014).
[7] M.B., M. Kolodrubetz and A. Polkovnikov, Phys. Rev. Lett., 116, 125301 (2016).
[8] P. Weinberg, M.B., L. D’Alessio, A. Polkovnikov, S. Vajna, and M. Kolodrubetz, Physics Reports, 688 1-35 (2017).
[9] D. Abanin, W. De Roeck, and F. Huveneers, Phys. Rev. Lett., 115, 256803 (2015).
[10] T. Mori, T. Kuwahara, and K. Saito, Phys. Rev. Lett., 116, 120401 (2016).
[11] M.B., S. Gopalakrishnan, M. Knap, and E. Demler, Phys. Rev. Lett., 115, 205301 (2015).
[12] S. Lellouch, M.B., E. Demler, and N. Goldman, Phys. Rev. X, 7, 021015 (2017).
[13] M.B., M. Heyl, D. A. Huse, and A. Polkovnikov Phys. Rev. B, 93, 155132 (2016).
Copyright © 2017 Marin Bukov