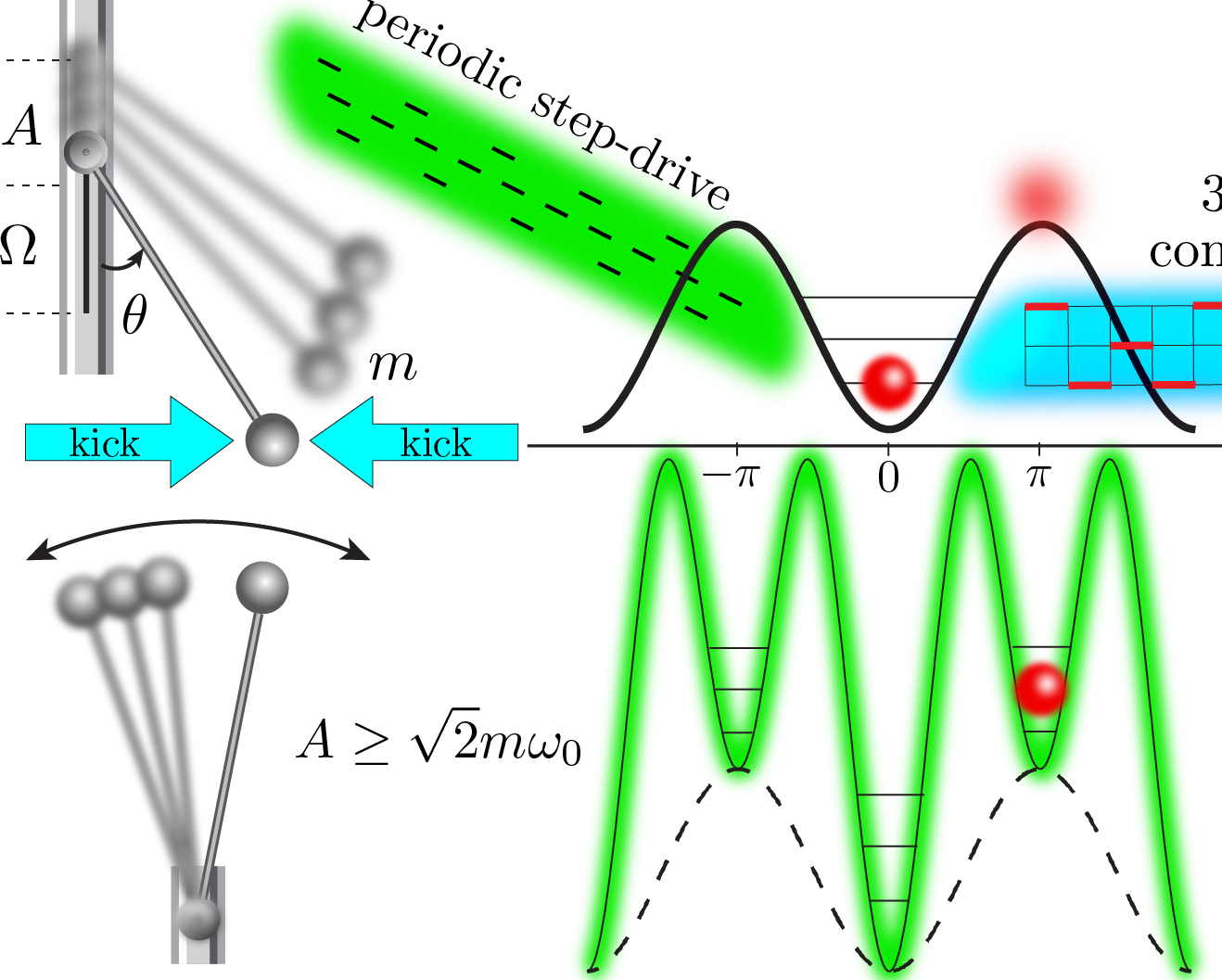
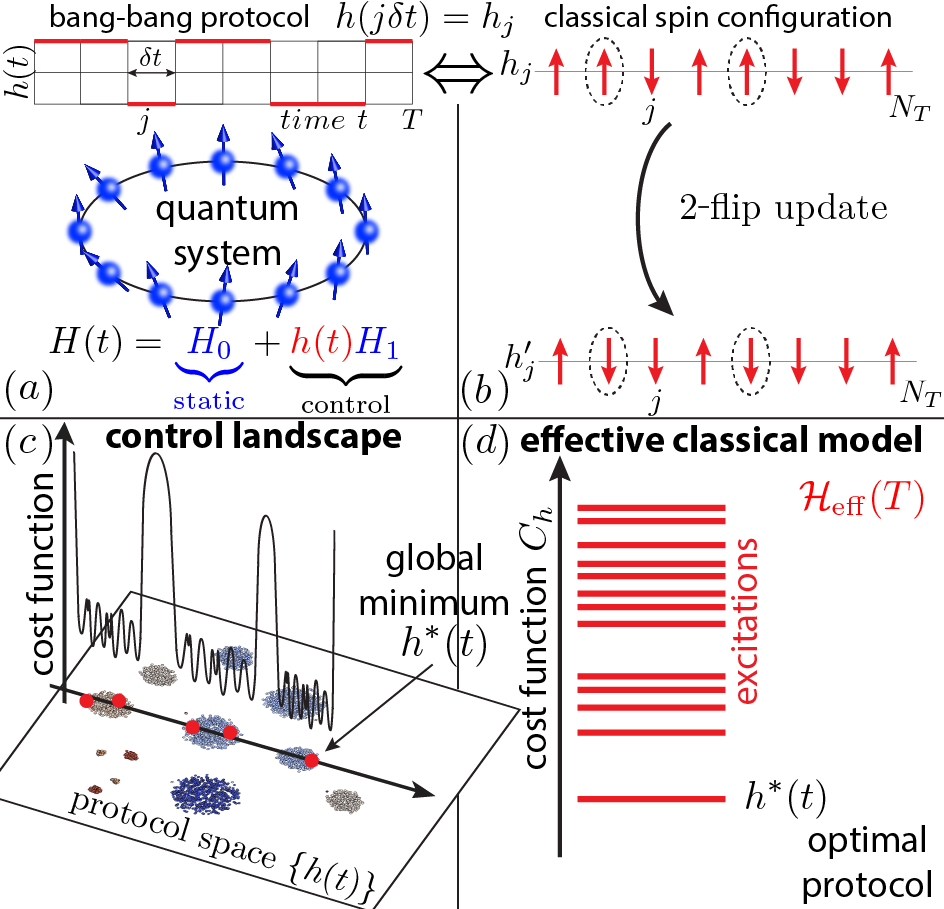
We present evidence for a universal spin-glass-like transition in the quantum control landscape, controlled by the control protocol duration. The glassy critical point is marked by a proliferation of protocols with close-to-optimal fidelity and with an optimal protocol that appears exponentially difficult to find.
Check out this paper for a more detailed and complete discussion [1].
|
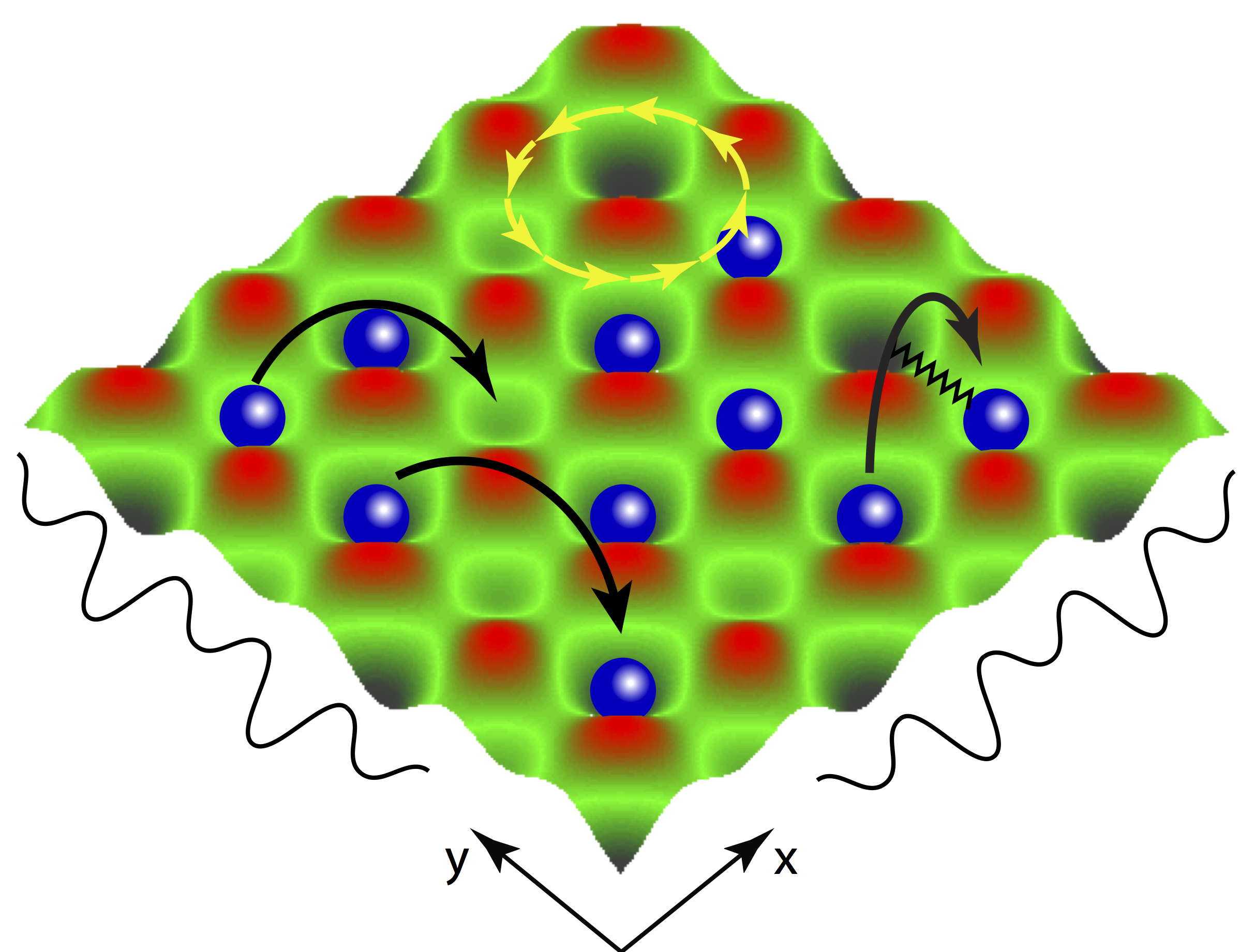
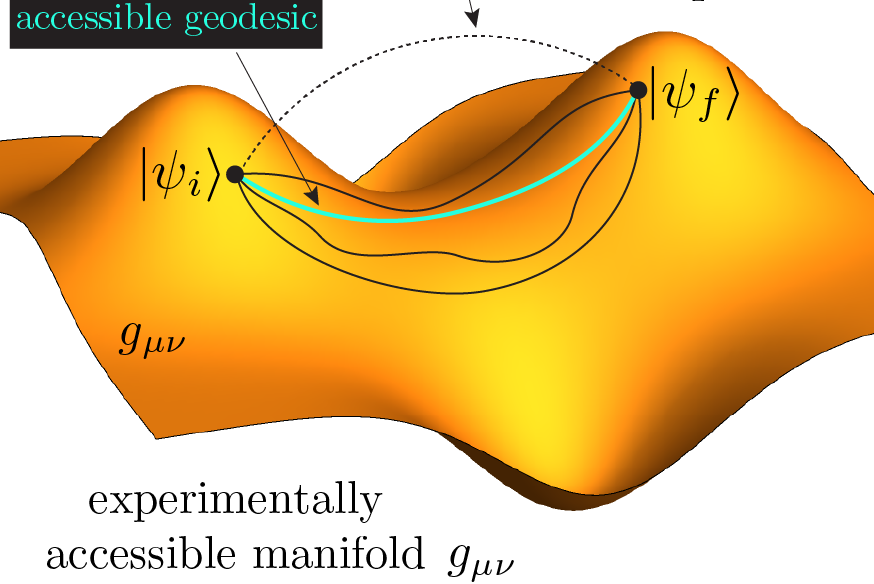
A major challenge in the quest for developing reliable quantum computing architectures is the ability to achieve high-precision quantum state control. To address this problem, a variety of optimal control algorithms have been developed. In our study, we reveal that the complexity of preparing correlated many-body states [see Fig, panel (a)] quickly and with high fidelity, can undergo drastic changes resembling phase transitions. We map the quantum control problem to a classical Ising model and apply concepts of statistical physics [see Fig, panels (b),(d)] in order to analyze the properties of these phase transitions of quantum control. In particular, we show strong evidence for the onset of a glass-like phase due to an underlying extremely rugged quantum control landscape [see Fig, panel (c)]. Using the machine learning technique t-SNE, we further show that the control transitions exhibit clustering in the space of local infidelity minima, a phenomenon familiar from spin-glass physics. This allows us to ultimately make a connection between quantum control and constrained satisfiability problems, which can be used to quantify the feasibility of optimal quantum control. Our study provides an exciting new direction of research in the area of overlap between nonequilibrium quantum dynamics, statistical physics, and machine learning.
References:
[1] A. G.R. Day, M.B., P. Weinberg, P. Mehta, and D. Sels, Phys. Rev. Lett. 122 020601 (2019).
[2] M.B., A. G.R. Day, D. Sels, P. Weinberg, A. Polkovnikov, P. Mehta, Phys. Rev. X 8 031086 (2018).
[3] M.B., A. G.R. Day, P. Weinberg, A. Polkovnikov, P. Mehta, and D. Sels, Phys. Rev. A 97, 052114 (2018).
Copyright © 2018 Marin Bukov